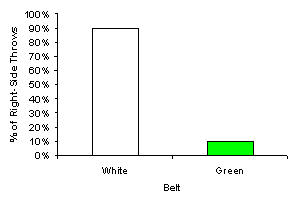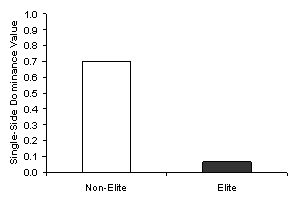by Susan Lee and Herbert Quan |
Abstract
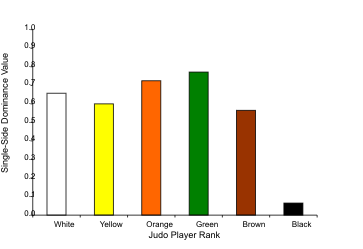
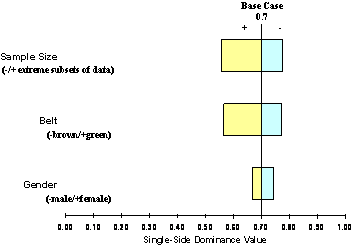
Hand Dominance of Elite Versus Non-Elite Judo Players Over 90% of a given population is right-handed, including the sports population. A right-handed person by definition tends to eat, write, open doors, answer the telephone, and “manipulate objects in everyday situations” (Mikheev, Mohr, Afanasiev, Landis, & Thut, 2001) with his or her right hand. When extending this finding to the sport of judo, one might expect that judo players would have a side bias determined by their handedness. Therefore, in a combative sport such as judo, one would expect to find that 90% of judo throws should be right-sided, ceteris paribus (other things being equal). The issue becomes more complicated in higher-level judo, because judo is more than a sport – it is also a grappling art discipline whereby handedness has the potential to affect the outcome of a judo match. The distribution of handedness directly affects a judo player’s behavior. If a judo player is aware that his or her opponent will always throw from the right, the judo player will be able to better anticipate the opponent’s strategy. (These hypotheses will be discussed later). Because handedness has the potential to affect outcomes in judo, one would expect to find that judo players throw with a different hand dominance distribution than what is found in the general population. In tachiwaza, which is the branch of judo concerned with throwing an opponent from a standing position (as opposed to newaza, which is the branch of judo concerned with ground fighting), opponents may be thrown from either a judo player’s right or left side (hip, shoulder, or leg).It should be understood that sidedness does not refer to the direction in which the opponent is thrown.Human anatomy remains constant; that is, the right or left side of the point of contact remains constant, but the direction of motion (of a throw) is always changing.Thus, an opponent can be thrown in any direction within 360°. “Right or left side” simply refers to the side of the thrower’s body that is used as the anchor in the throw. Typically, a judoist pressing an attack will take hold of an opponent’s jacket, belt, lapel, or sleeve; this grip precedes a throw. The first moment of contact can determine the outcome of the throw. “If you hold your opponent’s right sleeve with your left hand and his left lapel with your right hand, your throwing techniques will be limited to only the right side” (Watanabe and Avakian, p. 93).Thus, a judo player’s technical range is largely restricted by his or her throwing strategy. Restriction of a given technique to a single side will result in the loss of many opportunities for applying a throw. An assumption can be made, therefore, that the ability to throw from the right and left posture with close to equal proficiency has a greater pay-off than throwing from a single side, but that learning to attack in both directions is difficult to master. The Mikheev et al. (2001) study found that ambidexterity is a function of practice; therefore, it can be inferred that the ability to execute a throw from either side (or ambidextrousness in judo) is an acquired or learned characteristic. It is expected that overcoming one’s handedness requires a certain amount of time.In turn, it may be expected that beginning judo players will most likely exhibit more single-sided dominance. In contrast, if a right-handed judoist can execute left-handed techniques, then his or her range of techniques is increased by 100% (see Figure 1). A judoist who is proficient in throwing with both sides can perform twice as many techniques as a person who restricts himself to either left or right-handed techniques. A judoist’s strategy becomes exponentially more sophisticated as he or she acquires the ability to manipulate the opponent’s mass in multiple directions. According to Watanabe and Avakian, having an inherent side bias is a liability when doing judo. For this reason, one would expect to find that the right or left-handed dominance disappears or is mitigated at the elite levels. This prediction is validated by studies in game theory, which will be discussed later in this paper. Furthermore, not only is a judo player’s repertoire of techniques expanded by the ability to execute throws from both sides of his or her body, it will inevitably become necessary, if one wishes to win a match, to throw the opponent from one’s non-dominant side. Let one suppose that a judo player, or Player 1, attempts to throw his or her opponent using a right hip throw.The attempt itself unbalances Player 1.At the instant Player 1 makes the attempt, but before he or she has fully executed the throw, Player 1’s left flank is momentarily vulnerable to a reversal or counter; Player 2 can now counter Player 1’s throw by using a left side technique. If, however, Player 2’s skill set was restricted to right side techniques, he or she would not be able to adjust to the opponent’s body posture, consider the opponent’s inertia or otherwise use the opponent’s postural weakness to his or her own advantage, execute his or her own counter, and would most likely be defeated. Watanabe and Avakian (1960) give a description of the nullification of an opponent’s attack: “The judoist must not place himself in a situation where an effort to defend himself against his opponent’s suddenly changed position may leave him exposed to the attack” (p. 21). In theory, in a match between two judo competitors with all other factors being equal (strength, speed, stamina, weight, experience, age, etc.), the advantage of ambidextrousness in one judoist may be enough to force an immediate defeat against the judoist who trains to throw exclusively from his or her dominant side. The chances of winning a match with such a disadvantage appear to be inconsiderable. Literature Review Mikheev et al. (2001) conducted a study that investigated handedness and sports. Their study primarily focused on the relationship between handedness and brain function. Their study found that, although 90% of a given population is right-handed, self-reported right-handed athletes exhibit more ambidexterity than normal populations when carrying out activities that required repetitious action. In fact, athletes who were overall right-handed not only “preferred more frequently to perform certain movements with the left hand”, but they also revealed “enhanced right-hemispheric involvement” (Mikheev et al., 2001) in lateralized cognitive tasks. According to Mikheev et al. (2001), the right hemisphere controls both repetitious movements and left postural and manual routines, and in athletes, an overlapping effect occurs in which repetitious right-hand movements is associated with a greater hemispheric symmetry in visuo-spatial functions. The Mikheev et al. (2001) study suggests that ambidexterity in judo players is directly proportional to the prodigious number of repetitions that it takes to attain proficiency in any judo technique. In other words, long-term motor training is positively correlated to ambidexterity in judo players. While the Mikheev et al. (2001) study examined ambidexterity in sports in relation to brain function; an alternative approach is to use a game theoretical framework to explain ambidexterity as a conscious choice (or strategy, to use game theory terminology) made by the players. “Game theory is the mathematical study of human interaction as described by rules of play and alternative choices” (Levine, 2001); that is, game theory describes how people interact given discrete choices (strategies) and results of their interaction (payoffs). This framework is directly applicable to judo, because judo possesses elements of a “game”: strategy (players choose what type of throw, which side to throw, and when to throw) and payoffs (does a player win or lose?). The previous statement can be inferred from Levine’s (2001) description of game theory, in which he explicitly states that strategies and payoffs are fundamental to game theory. This particular experiment is concerned with only one dimension of a judoist’s strategy – whether the judoist throws with his or her right or left side. Therefore, in any one “game”, a judoist has two strategies: throw from the left or throw from the right. This game can be visually depicted in a game matrix (see Figure 2). In Figure 2, there are two judoists: Player 1 and Player 2. Both players have the same set of strategies (left or right throw). Each combination of strategies results in a payoff. The number on the left in each payoff box represents Player 1’s payoff; the number on the right represents Player 2’s payoff. In this simple representation, game theory seeks to answer the question: Given the player’s strategy sets and related payoffs, what is the optimal strategy (or best response, in game theory terms) for each player given that he or she knows what the strategy set and payoffs are for the other player? Referring back to Figure 2, each player has a strategy set of two strategies (right or left side throw). To the extent that each player has only one strategy available to him (for example, if he only throws from the right), the game has only one outcome. However, if the number of strategies doubles (each player can now choose to throw with the right or left side), then the number of possible outcomes quadruples (see Figure 3). Mathematically, the number of outcomes is equal to the number of strategies for one player squared if each player has the same number of strategies. Therefore the game becomes geometrically more complex. What makes throwing with the right or left side in judo important is that, to the extent that one player is limited to one strategy, the other player knows exactly how to react. One judoist can predict which strategy his opponent will choose, so the judoist can choose between two outcomes and maximize his payoff. To understand the application of game theory to how judo players select from which side to throw, it is useful to discuss a type of game known in game theory as Matching Pennies. What defines this game is the absence of a “best-response pure strategy” by either player (Goeree, Holt, & Palfrey, 2002). In other words, other game types are characterized by strategies and payoffs that incentivize each player to always choose the same strategy. The Matching Pennies game can be depicted in a game matrix (see Figure 4). Here, Player 1 and Player 2 both have the same strategy set, with each set consisting of two strategies: each can throw from either the left or the right. Assume that Player 1 will react before Player 2 (this is a sequential rather than simultaneous game), so Player 2 must anticipate whether Player 1 will throw with his/her right or left; Player 2 must counteract with a right or left technique of his/her own. This payoff structure is depicted with –1 and 1; -1 represents losing the judo match and 1 represents a win. The left value in each payoff box is Player 1’s payoff; the right value is Player 2’s payoff. Since Player 2 must anticipate Player 1’s strategy, the matrix depicts Player 2 winning if both players choose the same strategy. In the event that Player 2 does not correctly anticipate Player 1’s strategy, Player 1 wins the match. This particular game does not have a pure strategy because both Player 1 and Player 2 would not choose to always play the same strategy no matter what the other player chooses. In other words, both players have the incentive to randomly select whether to throw right or left with a 50/50 distribution (Roth, 1991). This randomization of choosing strategies is particularly significant since judo is a repeated game where contestants may be forced to attempt many throws before the match is over. The literature on game theory explains what happens if either Player 1 or Player 2 chooses a pure strategy rather than a mixed strategy. Game theory demonstrates that if Player 1 always chooses to throw with his right side, Player 2 would always be able to anticipate his strategy and choose the correct response (Goeree et al., 2002). Thus, Player 2 would always capture the higher payoff (see Figure 4). This outcome holds true even if Player 1 doesn’t choose a pure strategy but chooses to play one strategy more often than the other strategy (for example, Player 1 will throw with his right side 70% of the time and with his left side 30% of the time) (Figure 5). So in judo, players attempting to maximize their payoff over a series of matches will choose to use both right and left sides. Moreover, game theory literature suggests that not only will they choose to use both left and right sides; the players will seek to randomize which side to use with a 50/50 probability (Erev & Roth, 1998). Game theory literature also suggests that this mixed strategy will result in a zero payoff over the long run (they will win as many games as they lose), but that using any other strategy will result in a negative payoff, meaning that over the long run, they will lose more than they win (see Figure 5). The first hypothesis of this study was that non-elite (defined as non-black belt) judoists would tend exhibit single-sided dominance when throwing an opponent; this bias reflects the “stable over 90% right-handedness in a normal population across cultures and ages” (see study on motor control by Mikheev, et al.). If 90% of the general population were right-handed, one would expect to see that bias among judoists. Thus, the first purpose of this experiment was to determine if low-level or “non-elite” (defined in this study as being non-black belt level) judo players threw primarily from their right or left side, depending on their handedness. It is hypothesized that an elite judo player should have the ability to adapt and improvise based on the needs of the moment. If a right-handed judo player is in a position to counter a throw with a left side throw, and has not trained to do so, it is unlikely that he or she will ever reach the elite category. Accordingly, the second prediction of this study was that elite, high-level judo competitors (defined as participants in Olympic and International competitions) are more likely to overcome their inherent handedness and exhibit a more even distribution of right and left side throwing. Taken together, the present study was designed to investigate if elite judo players (those who compete in International and Olympic games) executed a comparatively more even distribution of right and left-side throws than the non-elite category. If the hypotheses of this research are correct, then equivalencies in a judoist’s throwing side preference will emerge as he or she grades to the elite level. Method Participants This study used 277 data points derived from 135 subjects, aged 16 and over.The number of male elite subjects was 47; female elite subjects, 30; male non-elite subjects, 39; and female non-elite subjects, 19. 58 subjects were non-elite white through brown belts, from whom the data were gathered through naturalistic observation; 77 subjects were elite black belts who participated in Olympic and World Championships, from whom the data were gathered through videos. Apparatus A tallying procedure was used to record information on identical data sheets for each right and left-side throw.The data were grouped into the category of six belt classes, each belt class subdivided by gender, and each gender subdivided again into left and right side (see Appendix 1).A single tally mark was made in the appropriate space.The video archives from which the data were gathered are available at www.judoinfo.com. Procedure A data sheet was prepared, duplicated, and distributed to all the experimenters. Experimenters visited several judo clubs in the local area, and if given a formal welcome, introduced themselves as prospective students of judo who wished to observe a class. Observers are commonly seen during practice; their presence generally does not distract. However, a self-identified researcher might have caused the emotional discomfort of judoists and the instructors. The experimenters feared that stating the true purpose of the visit would produce suspicious reactions, possibly even causing the judoists to be guarded and highly self-conscious during practice even if consent forms were administered first. Experimenters waited through the warm-up exercises and uchi komi (throwing drills). Only during randoriwere data sheets brought out, and tallying began. By that time it was expected that the judoists were fully committing their attentional resources to defending against or overpowering an opponent, and would take much less notice of the experimenters than if the experimenters had produced the data sheets before practice. The rules for collecting data were as follows, and applied to observations made both from the dojos and videos: 1. Observations were made during standing randori only, and of shoulder, hip, and leg tachiwazaonly. The practice of randori, which translates into free practice, distinguishes judo from most other martial arts. Instead of practicing pure kata, which means form, or “a system of prearranged movements that teaches the fundamentals of unarmed attack and defense” (Kano, p. 20), judoists “pair off and vie with each other as they would in an actual match” (Kano, p. 22). Data were collected only during standing matches, and only for shoulder, hip, and leg tachiwaza(throwing techniques done in a standing position). The rationale was that the large, circular movements of throwing are much easier to identify than the subtler maneuvers seen in joint locks, hold-downs, strangleholds, or two entangled, prostrate opponents engaged in a ground fight. In a shoulder throw, the shoulders of the opponent and the thrower meet; the thrower rolls the opponent over his or her body using the shoulder as the primary point of contact. In a hip throw, the hips of both contestants meet, and the thrower rolls the opponent over his or her body using either hip as the point of contact.In a leg sweep, the thrower uses his or her leg(s) to trip the opponent or reap the opponent’s legs from under him. 2. Two experimenters did not observe the same judoist simultaneously. This was to prevent two observations of the same event, thus weighting the event more heavily than others. 3. If the throw was not “clean”, the observation was still valid as long as the throw was fully executed and the intent to throw was recognized. The rationale was the idea that the study did not set out to measure a judoist’s ability to execute a technique. If a judoist attempted a throw, and his or her intent was recognized, the judoist was still attempting to execute a strategy. For the purposes of this study, strategy was defined not as the ability to execute a technique, but the planned intent, even if it failed. 4. If an experimenter was uncertain which side the judoist used to execute the throw, an observation was not recorded. 5. Experimenters attempted to record one observation per judoist until all judoists had been observed before rotating back to judoists he or she had already observed. It was reasoned that the experimenters should attempt to gather as many data points from as many subjects as possible in order to avoid a possible bias. For instance, data collected solely from a particular white belt who might have had a long acquired, or inherent ability to use both hands with equal facility would have skewed the results. Results The objective of the present research work was to determine if non-elite judo players reveal a single-side bias in throwing, and if elite judo players reveal a comparatively more even distribution of left and right side throws than non-elites. The most intuitive metric to use for this study would be the measure of frequency with which a judo player throws using either his or her right or left side.In other words, one would tally all throws made by each belt class and create a bar chart of the percentage of right-side throws by belt class (Figure 6). However, using this metric could potentially produce misleading results if the random sample of judo players exhibited systematic biases that were different between belts. For example, let one suppose that there are 4 green belts and 4 white belts in the data set (Figure 6). The white belts are right-handed, the green belts left-handed. Assume 90% of throws executed by the white belts are right-sided (right-side bias) and 10% of the throws executed by the green belts are right-sided (left-side bias). A bar graph representing number or percentage of right-hand throws would show a vast difference between the two groups (see Figure 6). The results would show that 90% of throws executed by white belts are right-handed, and 10% of throws executed by green belts are right-handed when in actuality, both belt classes preferred to use a single chosen side 90% of the time. The problem with using such a metric (number or percentage of throws that are right-sided) is that it takes into account whether the throw is right or left-sided rather than measuring if a thrower has a dominant side, no matter what that side is. In other words, the appropriate metric to use must not discriminate between left and right sides, but should discriminate between whether judo players tend to throw with one or both sides. Accordingly, the Single-Side Dominance Value (or SSDV) (see Figure 7) was developed. Rather than asking how often a judo player threw with his or her right or left side, the metric was aimed at determining the propensity of a judo player to throw with a single side (left or right) versus utilizing both sides. The SSDV metric possesses a scale (unit of measurement) from 0 to 1 so that it allows one to have a good sense of the order of magnitude of the measurement similar to other scales that measure relative variables rather than absolute metrics. A score of 1 means that a judo player throws only with one side, and a score of 0 indicates that the judo player shows an equal balance of right and left side throws. To calculate the SSDV, one takes the absolute value of the difference between the percentage of right and percentage of left hand throws (Figure 7). The results of this study show that 85% of the throws executed by the non-elite category are right-side throws, and 15% of the throws are left-side throws. These observations result in an SSDV of 0.70. In contrast, 53% of the throws executed by the elite category are right-side throws, and 47% of the throws are right-side throws, which results in an SSDV of 0.06 (see Figure 8). The data revealed that there was a difference of 0.64 in the SSDV between the elite and non-elite categories, or non-elites had a propensity twelve times greater (0.70/0.06) than that of elites to rely on a single side when throwing. The blue belts were excluded when looking at the data by belt class, due to the fact that the sample size of the blue belts was too small to give meaningful results. There were a total of five observations for the blue belt class when there was a minimum of 15 observations for the other belt classes, and a mean of 45 observations across all non-blue belt classes. Note that the blue belt class was not excluded from the elite versus non-elite analysis because the blue belt observations were simply aggregated into the non-elite category. When looking at the data by belt class (see Figure 9), the SSDV for the non-elite belt classes (white, yellow, orange, green, and brown) were within a bandwidth of 0.57 and 0.77. The mean SSDV between non-elite belt classes was 0.66; the median was 0.66; and no mode existed for the data because each belt class had a different value. This differs from the aggregated non-elite SSDV of 0.70 because the aggregated non-elite figure was a count of individual throws equivalent to the weighted average of the belt classes, which also included the blue belt class for this calculation (see Figure 10). The standard deviation between the non-elite belt classes was 0.08, or 11% of the mean. These results were statistically significant because the elite SSDV was eight standard deviations away from the non-elite SSDV. Discussion The high SSDV of the non-elite category indicates that the first hypothesis is true; an association between single side dominance and handedness exists. This study would seem to support the Mikheev et al. (2001) findings that about 90% of a given population are right-handed. From the first hypothesis, one would expect that non-elite judo players would exhibit an SSDV close to .80 (see Figure 8). The mean SSDV of the non-elite category was 0.70, which was close to the predicted value. This also indicates that some marginal effort was made by the non-elites to throw with their non-dominant side, which may account for the 0.10 differences between predicted and actual values. The low SSDV of the elite category indicates that elite judo players do indeed throw with an almost perfectly even distribution between right and left sides. This result was very close to the predicted value of 0.00 (see Figure 11), and suggests that elements of ambidexterity are important in high-level judo because the use of both left and right side throws improves performance and results in a higher payoff than a strategy that limits throwing to a single side. These empirical results confirm the predictions made in game theory literature regarding the frequency of right and left hand throws. The almost perfect balance of right and left side throws exhibited by the elite judo players mimics the results of the Matching Pennies game cited in the literature. An alternative explanation for the results is that, for one reason or another, judo favors left-handers. At the low levels, the judo population is still representative of the general population when it comes to handedness, but as one examines the higher levels, the judo population becomes disproportionately left-handed. A self-selection process might occur in which left-handers find it easier to progress to higher levels of judo, where at the elite level the proportion of left and right-handers happens to settle at a 50/50 equilibrium. Such a process would create results similar to the ones found in this study. This explanation, however, contradicts Mikheev et al.’s (2001) findings that ambidexterity in judo players emerges as a result of over-training. This study could have been improved in three ways. An implicit assumption was made that the population of judo players is representative of the general population when it comes to right or left-handedness; that is, 90% of judo players are right-handed. Future studies could incorporate a survey of a random sample of judo players to determine if this assumption is true. If the assumption were not true, then alternative explanations as to why non-elite judo players exhibit an SSDV close to 0.80 would need to be explored. The second way this methodology could be improved is by increasing the sample size across all belt classes such that statistically significant results could be extracted. For instance, in this study the blue belt class had to be excluded from the belt-by-belt analysis because of its small sample size. The third way this study could be improved would be to control for the variables mentioned in a hypothesis in the introduction of this paper regarding strength, speed, stamina, weight, experience, age, etc.These factors could largely be controlled by observing non-elites at actual competition (instead of practice), where age and weight categories determine which players compete with others. The main challenge of the present study was that one of the experimenters with no martial arts background reportedly found it difficult to determine throwing side while observing judo due to the speed of the action and often imprecise throwing techniques. However, this factor did not prove to be a hindrance while gathering data from video archives because the experimenters were able to replay matches; also, this data were gathered by the remaining experimenters who possessed some martial arts experience. The tornado diagram (see Figure 12) was used to demonstrate the sensitivities of the study’s results to certain variables (sample size, belt level, and gender), with two extremes off the mean for each variable. The diagram shows that if two data sets were chosen that deviated most off the mean SSDV of .70, the results would have shown a small downside potential. The SSDV that deviated farthest from the mean was 0.56, which was 0.14 away from the base case SSDV. The results would have been interpreted thus: all non-elite judo players had a medium propensity to throw with one side; or, non-elites did not appear to be completely committed to throwing using a single side, yet were not completely balanced in throwing with both sides. However, the actual result showed relatively very little variation – only .14 – between large and small sample sizes. There was not a huge variation on the SSDV, and a 0.14 difference did not even remotely change the result. When using all data sets, and thereby increasing the sample size, observations revealed that non-elite judoists have a high propensity to throw with one side. A larger sample size brings one closer to the more correct answer because it reduces the amount of sampling error. In the future, another study can be done that uses data from an even greater sample size in order to minimize sampling error. The results were even less sensitive to the belt class variable. When looking at the two data sets with the greatest variation off the mean (brown and green belts), one does also not observe wildly different results. Finally, if gender were observed discretely, the results would be even closer to the base case SSDV than the other variables. Of all the variables to which this study was sensitive, gender mattered least in terms of the results. Altogether, this diagram shows that this study was not highly sensitive to sample size, belt level, or gender. The results were fairly consistent whether all data sets were observed, or just the data set with the greatest value away from the mean; all belt ranks or only a single belt class, or only females or males. If this study were to be repeated, future experimenters should arrive at an even smaller error range if data were collected from a larger sample size. In future studies, it might be interesting to look at other sports where handedness may have an influence on the results of the sport. One might also wish to explore where in a skill level continuum the break point exists between when players exhibit a high SSDV and a low SSDV. References Ekev, T., & Roth, A.E. (1998). Predicting How People Play Games: Reinforcement Learning in Experimental Games with Unique, Mixed Strategy Equilibria. The American Economic Review, 58-73. Georee, J.K., Holt, C.A., & Palfrey, T.R. (2002). Risk Averse Behavior in Generalized Matching Pennies Games. The American Economic Review, 19-34. Kano, J. (1986). Kodokan Judo. Tokyo: Kodansha International, Ltd. Levine, D.K. (2001). Introduction to the Dynamic Games. Review of Economic Dynamics, 19-26. Mikheev, M., Mohr, C., Afanasiev, S., Landis, T., & Thut, G. (2002). Motor Control and Cerebral Hemispheric Specialization in Highly Qualified Judo Wrestlers. Neuropsychologia 40, 1209-1219. Roth, A.E. (1991). Game Theory as a Part of Empirical Economics. Economic Journal, v.101, 107-114. Watanabe, J., & Avakian, L. (1960). The Secrets of Judo: a Text for Instructors and Students. Boston: Charles E. Tuttle Co., Inc. Figures Figure 1. Mathematical representation of how learning right and left side throws doubles the number of single-side techniques. å[N(TR) + N(T L)] = 2N Where N = number of techniques in a given set TR = {t1, t2, t3…tn} where TR is a set of right-handed techniques TL = {t1, t2, t3…tn} where TL is a set of left-handed techniques TR = TL Figure 2. Generic game matrix form of a judo match.
where P = various undefined pay-offs Figure 3. Mathematical relationship between number of strategies and number of outcomes in a judo match. R = N(P1) x N(P2) where R = number of outcomes N = Number of strategies in a given set P1 = strategy set of Player 1 P2 = strategy set of Player 2 Figure 4. Game matrix depicting Matching Pennies.
If Player 1 chooses a pure strategy (right, for instance), Player 2 will also always choose right and win the match. Figure 5. Expected value of a mixed strategy if Player 1 does not randomize right and left throws with a 50/50 balance; refer to Figure 4 for game form and pay-offs. Given Player 2 chooses a pure strategy in response to Player 1 not randomizing strategies with a 50/50 balance: E(V) = p*(R) + (1 – p)*(L) where, E(V) = expected value p = probability Player 1 will employ right-side strategy 1 – p = probability Player 1 will employ left-side strategy R = right-side strategy pay-off L = left-side strategy pay-off For Player 1, if p = 0.7 1 – p = 0.3 R = -1 L = 1 then E(V) = 0.7*(-1) + 0.3*(1) = -0.4 For Player 2, if p = 0.7 1 – p = 0.3 R = 1 L = -1 then E(V) = 0.7*(1) + 0.3*(-1) = 0.4 Therefore, Player 1 E(V) < Player 2 E(V) Figure 6. Erroneous depiction of side dominance.
Figure 7. SSDV formula. SSDV = ½TR/TT – TL/TT½ Where TR = number of right side throws TL = number of left side throws TT = total number of observed throws Figure 8. Elite v Non-Elite SSDV.
Figure 9. SSDV results by belt excluding Blue Belts.
Figure 10. Weighted average SSDV of non-elites. Weight is determined by dividing number of observations per belt by total observations (200).
Figure 11. Predicted value of elite and non-elite SSDV. Hypothesis One: Non-elites exhibit single-side dominance that reflects population hand dominance (90% right-handed, 10% left-handed). Out of a sample 100 observations: SSDV = ½90/100- 10/100½ = 0.8 Hypothesis Two: Elite judo players exhibit an even distribution of right and left-side throws. Out of a sample 100 observations: SSDV = ½50/100- 50/100½ = 0.0 Figure 12. Tornado diagram of tested sensitivities. Appendix 1. Data from observations.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||